Many investors never evaluate their investment performance beyond simply noting gains and losses. Perhaps this is because they are not aware of how to conduct a proper evaluation. A couple basic calculations can help you better assess your portfolio returns and your financial advisor.
A growth calculation is quite simple for the portfolio that never has external contributions or withdrawals (ending value divided by beginning value minus one). The problem is that such portfolios seldom exist because investors frequently move their funds into and out of cash. This activity complicates the return calculation.
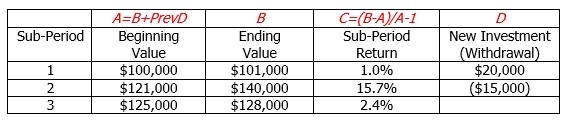
For instance, an investor who starts with an investment of $100,000 contributes another $20,000 when his portfolio is at the four month mark and valued at $101,000. At the nine month mark the portfolio value is $140,000 before the investors withdraws $15,000. At year end, the investor’s portfolio has a balance of $128,000. What was the investor’s total return?
The Time Weighted Rate of Return (TWRR) or Money Weighted Rate of Return (MWRR) can be used to make this calculation. However, the measures give different results and are applicable for only certain assessments.
Time Weighted Rate of Return (TWRR)
For the above example, TWRR identifies three sub-periods and calculates a sub-period return for each period. It then links these sub-period returns for an overall, total period return. Return for each period is ending value divided by beginning value minus one. New contributions or withdrawals are excluded from each period’s ending value and included in the subsequent period’s beginning value. Specifically, the sub-period returns are calculated as:
TWRR then calculates total return by linking returns from each sub-period’s return as follows:
(1+0.01) x (1+0.0157) x (1+0.024) – 1 = 0.0504 or 5.04% total return.
TWRR is appropriate when the investor wants to know how the mix of underlying investments performed. It ignores additional returns that might be gained or lost through the timing of new investments or withdrawals. This calculation is most relevant when assessing a portfolio or manager that has no influence over when to invest funds or, at least, isn’t trying to capture the effects of timing. Its primary disadvantage is that it requires careful record keeping, including the funds value at the end of each sub-period when new funds are invested or withdrawn.
Money Weighted Rate of Return
Unlike TWRR, Money Weighted Rate of Return does account for the timing of funds moved into and out of the portfolio. This accounting is important for investors who believe they can time the market to earn excess returns (e.g. invest just before market increases and sell before declines).
The MWRR does this by calculating the Internal Rate of Return (IRR) for each contribution to the portfolio. For the above example, the monthly rate is calculated by solving for R in the following equation:
$100,000(1+R)^12 + $20,000*(1+R)^9 – 15,000*(1+R)^4 = $128,000
The first term is the initial investment of $100,000, invested for a full year. The second investment of $20,000 occurs at the beginning of the fourth month (invested for eight months). The third term captures a withdrawal of $15,000 at the beginning of the ninth month (four months remaining). Solving for R (either using iterative guesswork or a financial calculator) gives a monthly return of 0.94%, an annualized return of 11.91%.
This 11.91% calculation is much different from the 5.04% return calculated above. This is because the MWRR captures the effect of investing $20,000 just before a growth and withdrawing $15,000 before a period of slow growth. Another major advantage of MWRR is that record keeping is easier. The only inputs into the model are beginning and ending values and the amounts and dates of contributions and withdrawals.